Leetcode 动态规划专题

1.斐波那契数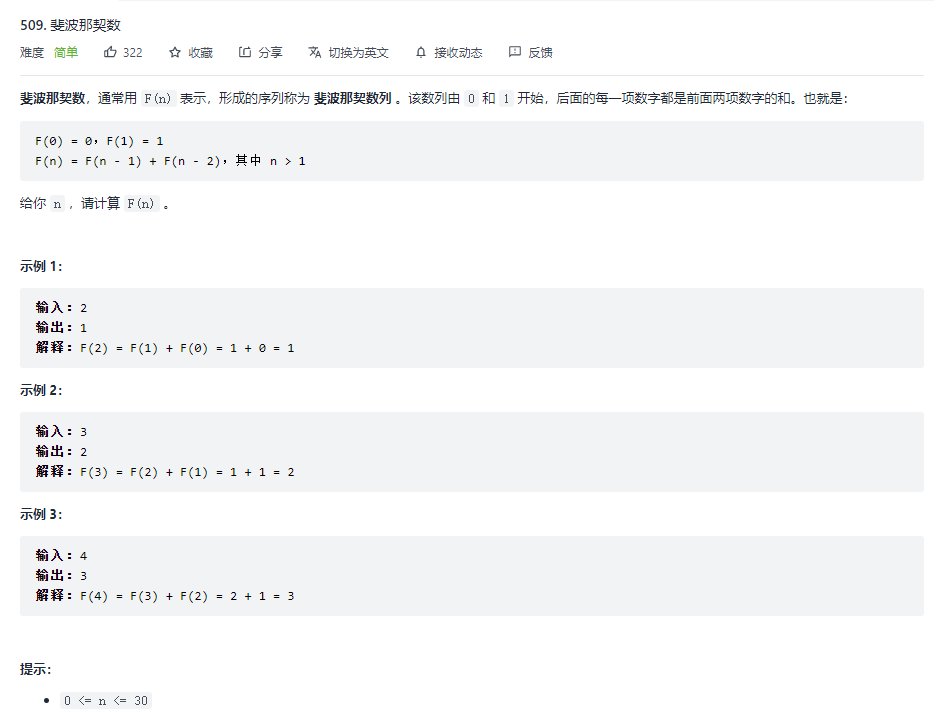

一.常见的递归解法

public int fib(int n) {
    if(n == 0){
        return 0;
    }
    if(n == 1){
        return 1;
    }
    return fib(n-1) + fib(n-2);
}

此方法严重浪费内存和时间，可利用数组对其优化.

二.数组解法

    if(n == 0){
        return 0;
    }
    if(n == 1){
        return 1;
    }
    int[] ans = new int[n];
    ans[0] = 0;
    ans[1] = 1;
    int i = 2;
    for(; i < n; i++){
        ans[i] = ans[i-1] + ans[i-2];
    }
    return ans[i-1] + ans[i-2];
}

三.迭代解法(此方法最好,内存占用为o(1)常数级)

public int fib(int n) {
    if(n == 0){
        return 0;
    }
    if(n == 1){
        return 1;
    }
    int x = 0;
    int y = 1;
    int ans = 0;
    for(int i = 2; i <= n; i++){
        ans = x + y;
        x = y;
        y = ans;
    }
    return ans;
}

2.使用最小花费爬楼梯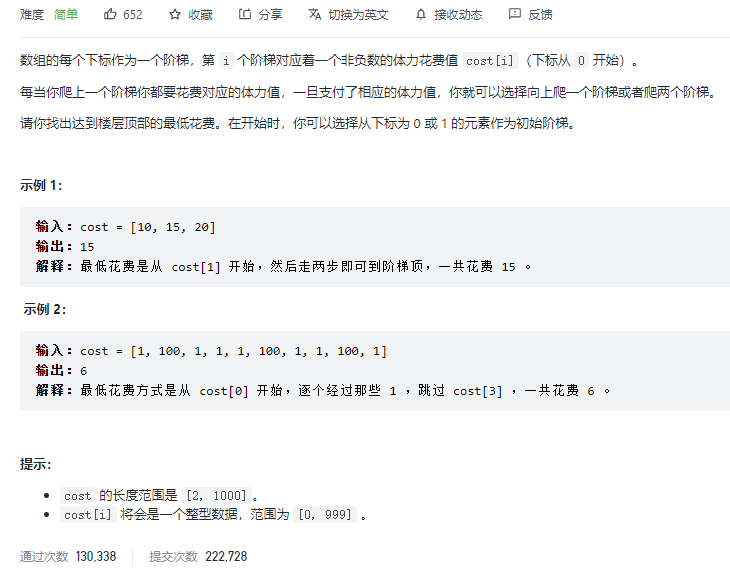

public int minCostClimbingStairs(int[] cost) {
    int[] dp = new int[cost.length];
    dp[0] = cost[0];
    dp[1] = cost[1];
    for(int i = 2; i < cost.length; i++){
        dp[i] = Math.min(dp[i-1],dp[i-2]) + cost[i];
    }
    return Math.min(dp[cost.length-1],dp[cost.length-2]);
}

3.打家劫舍(ps:这道medium题居然花不到10分钟自己写出来了...)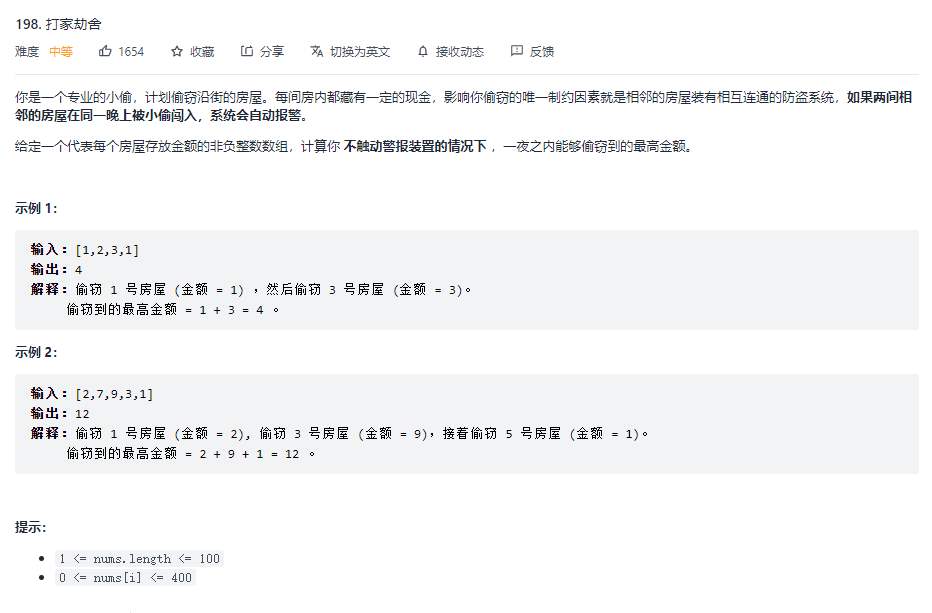

public int rob(int[] nums) {
    int len = nums.length;
    if(len == 1){
        return nums[0];
    }
    if(len == 2){
        return Math.max(nums[0],nums[1]);
    }
    int[] dp = new int[len];
    dp[0] = nums[0];
    dp[1] = nums[1];
    dp[2] = dp[0] + nums[2];
    for(int i = 3; i < len; i++){
        dp[i] = Math.max(dp[i-2],dp[i-3]) + nums[i];
    }
    return Math.max(dp[len-1],dp[len-2]);
}